Jul 28 2018

Pythagorea Set 7 Parallelograms Walkthrough and Answers

Walkthrough, solutions, and answers for Pythagorea, a puzzle game in the Google Play and Apple iTunes store. This is the full solution, answer, and walkthrough for set 7, Parallelograms. Follow along by downloading the app, and see the rest of the solutions at the bottom of this walkthrough!

For this walkthrough (solution, answer) for Pythagorea, the final solution will be shown. These can be seen as the final solution as the lines or dots are glowing orange.

Pythagorea Walkthrough Set 7, Parallelograms

Level 1

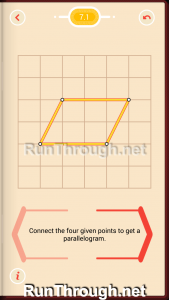
Level 2

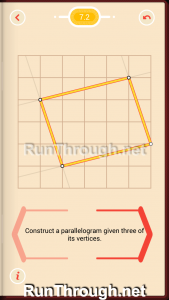
Level 3

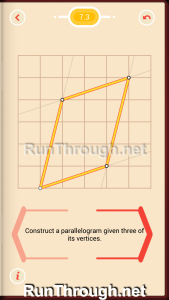
Level 4

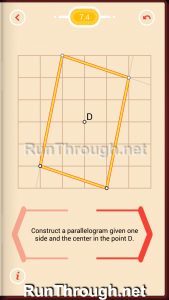
Level 5

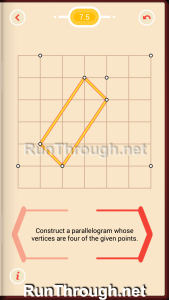
Level 6

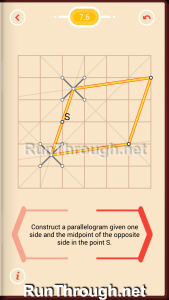
Level 7

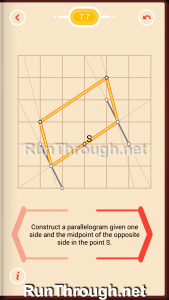
Level 8

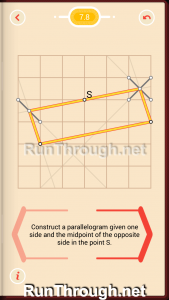
Level 9

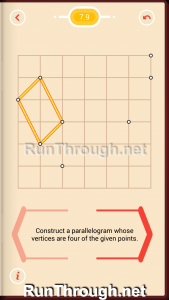
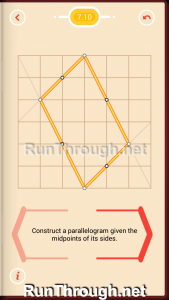
Level 10

Download: Google Play | iTunes

All Sets: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |19 | 20 | 21 | 22 | 23 | 24 | 25 | 26

See Pythagorea Review

Pythagorea Parallelograms

According to Math Planet a parallelogram is:

There are six important properties of parallelograms to know:

Opposite sides are congruent (AB = DC).
Opposite angels are congruent (D = B).
Consecutive angles are supplementary (A + D = 180°).
If one angle is right, then all angles are right.
The diagonals of a parallelogram bisect each other.
Each diagonal of a parallelogram separates it into two congruent triangles.

Fun facts about the parallelograms used in Pythagorea, according to Sciencing are:

Rectangles and squares are examples of parallelograms that have 90 degree angles, also known as right angles. Rhombuses and squares are examples of parallelograms that have sides of equal length.
Opposite interior angles of a parallelogram are always equal. For example, if one interior angle measures 36 degrees, the opposite interior angle will also measure 36 degrees. Consecutive interior angles in a parallelogram — angles that are side by side — are supplementary. That means that when you add two interior consecutive angles together, the total always equals 180 degrees. When you add all four interior angles together, the total always equals 360 degrees.
The diagonals of a parallelogram — lines that extend from one corner to the opposite corner — bisect one another. In other words, each diagonal cuts its opposite diagonal into two equal parts. No matter how you reshape a parallelogram, such as making the sides shorter or longer or increasing and decreasing the height, the diagonals will always bisect one another.